Draw Conditional Multivariate Normals

Fast way to draw conditional multivariate normals when the covariance matrix is sparse.

rmvnorm.conditional(n, y, mu = rep.int(0, dim(SigmaXX)[1]+dim(SigmaYY)[1]),
                    SigmaXX, SigmaYY, SigmaXY, noise, RstructYY = NULL, ...)

Arguments

n

number of observations.

y

observed vector.

mu

mean vector.

SigmaXX

covariance of X, required (of class spam).

SigmaXY

cross-covariance of X-Y, optional (of class spam).

SigmaYY

covariance of Y, required (of class spam).

noise

observational noice of Y, optional. See ‘Details’.

RstructYY

the Cholesky structure of SigmaYY.

...

arguments passed to chol.

Details

Quite often, we want to draw condional observations \(X|y\) from the model \(Y=X+e\), where \(X\) has covariance matrix SigmaXX and \(e\) has white noise.

Covariance of \(Y\) can be specified by SigmaYY or SigmaXX+diag(noise,). If \(Y\) and \(X\) do not have the same dimensions, SigmaXY needs to be specified.

The function also implmements a general multivariate model, where the we only observe part of the vector. The components are first \(X\) then \(Y\).

The function rmvnorm.cond() is a wrapper to rmvnorm.conditional() and included to increase similarities with other packages.

See also

rmvnorm.spam.

Author

Reinhard Furrer

Examples

set.seed(12)
N <- 300
y <- c(5, -5, -5, 5)
SigmaXX <- as.spam(.95^abs(outer(1:N, 1:N, "-")), eps=1e-4)
sel <- c(10, 100, 120, 300)        # where we observe y
SigmaXY <- SigmaXX[, sel]
SigmaYY <- SigmaXX[sel,sel] + diag.spam(.01, length(y)) # some noise
x <- rmvnorm.conditional(3, y, SigmaXX=SigmaXX, SigmaXY=SigmaXY,
                         SigmaYY=SigmaYY)
# unconditional sample:
ux <- rmvnorm(1, Sigma=SigmaXX)
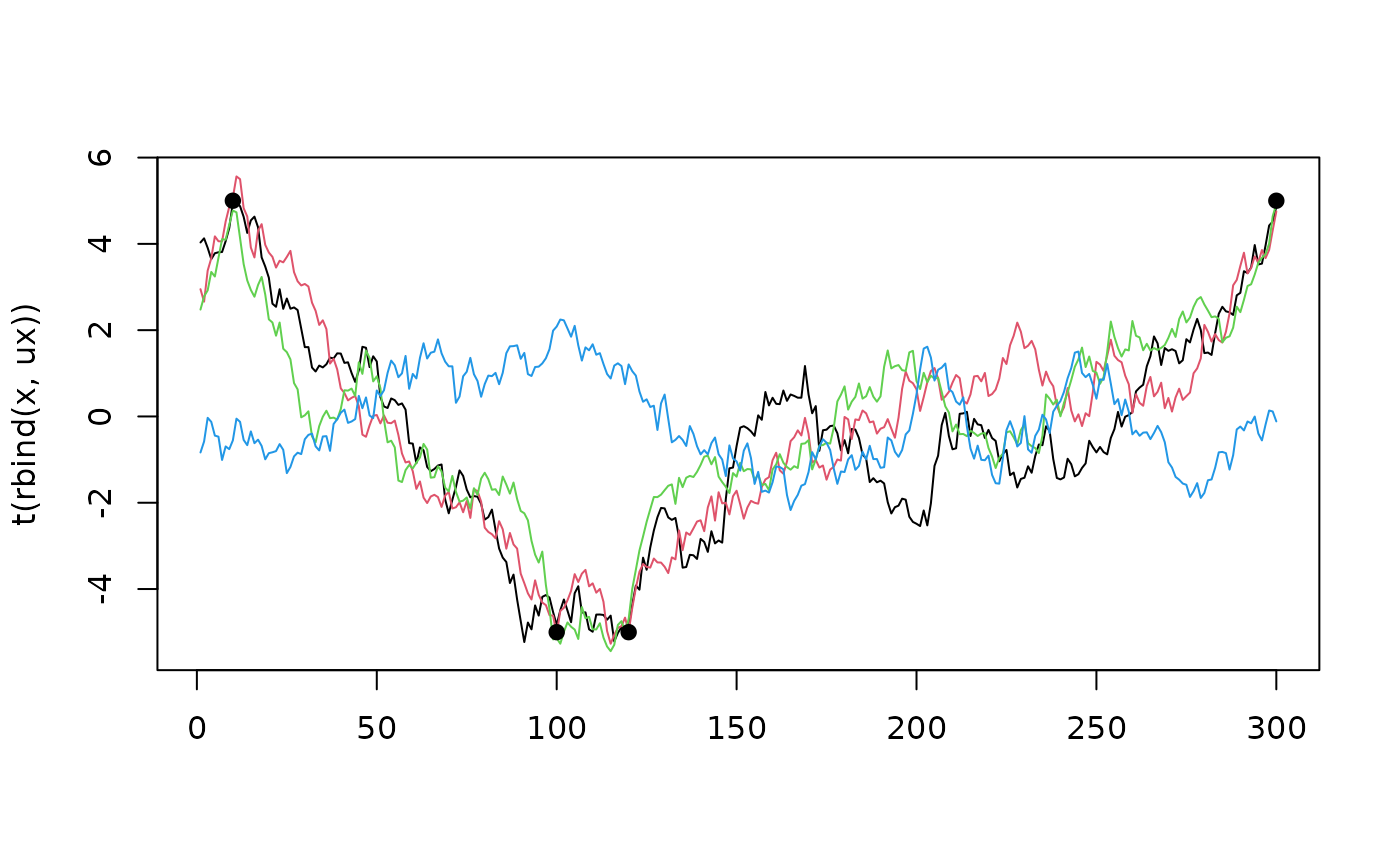
matplot(t(rbind(x, ux)), type='l', lty=1)
points(sel, y, pch=19)